Problemas Resueltos - Razonamiento matemático
Problema 85
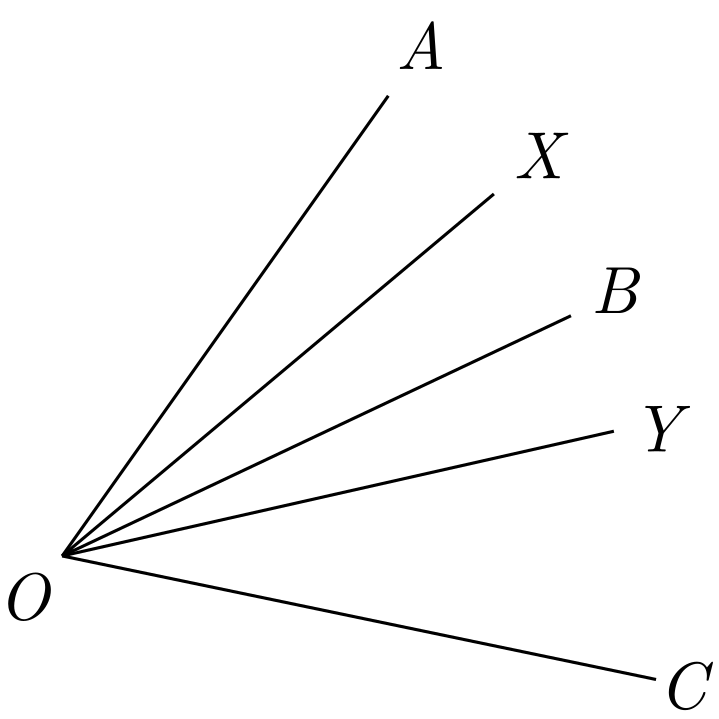
En la figura, \( \overline{OX} \) es la bisectriz del ángulo \( \angle AOB \), \( \overline{OY} \) es la bisectriz del ángulo \( \angle AOC \). Se sabe que el ángulo \( \angle AOB \) mide \( 20^{\circ} \) y el ángulo \( \angle BOC \) mide \( 30^{\circ} \), entonces el ángulo \( \angle XOY \) mide, en grados:
-
\( 15 \)
-
\( 10 \)
-
\( 5 \)
-
\(20\)
-
\(25\)
Intenta resolverlo antes de ver la respuesta...
-
\(15\)
Sean:
- \( \angle XOB = \alpha \)
- \( \angle BOY = \beta \)
- \( \angle YOC = \theta \)
Como \( \overline{OX} \) es bisectriz del ángulo \( \angle AOB \) y este mide \(20^{\circ}\), entonces \( \alpha = 10^{\circ} \)

Como \( \overline{OX} \) es bisectriz del ángulo \( \angle AOB \) y este mide \(20^{\circ}\), entonces \( \alpha = 10^{\circ} \)
Pero:
\[ \begin{aligned} \angle{AOC} &= \angle AOB + \angle BOC \\[1em] &= 20^{\circ} + 30^{\circ} = 50^{\circ} \end{aligned} \]Como \( \overline{OY} \) es bisectriz del ángulo \( \angle AOC \) y este mide \( 50^{\circ} \), entonces \( \theta = 25^{\circ} \)
Pero,
\[ \begin{aligned} \beta &= \angle BOC – \theta \\[1em] &= 30^{\circ} – 25^{\circ} = 5^{\circ} \end{aligned} \]Por último:
\[ \begin{aligned} \angle XOY &= \alpha + \beta \\[1em] &= 10^{\circ} + 5^{\circ} = \boldsymbol{15^{\circ}} \end{aligned} \]
