Problemas Resueltos - Razonamiento matemático
Problema 84
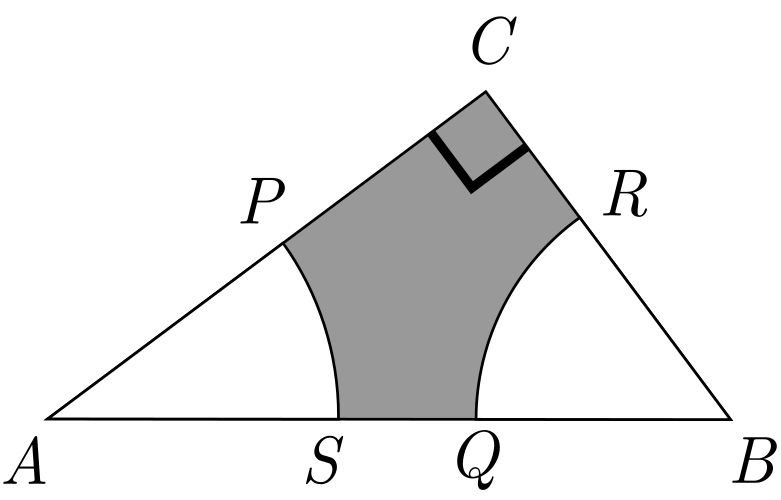
El triángulo \( \triangle ABC \) es isósceles y rectángulo en \( C \), con \( \overline{AC} = \overline{BC} = 12 \, cm \). \( \overset{\LARGE\frown}{PS} \) y \( \overset{\LARGE\frown}{RQ} \) son arcos de centro \(A\) y \(B\) respectivamente, y de radio \( 6 \, cm \). El área, en \( cm^2 \), de la figura sombreada es:
-
\( 6 (12 - \pi) \)
-
\( 3 (24 - 3\pi) \)
-
\( 3(48 - \pi ) \)
-
\( 8(9 - \pi) \)
-
\( 4(18 - \pi) \)
Intenta resolverlo antes de ver la respuesta...
-
\( 3 (24 – 3\pi) \)
Si \( A_S \) es el área de la figura sombreada, \( A_T \) es el área del triángulo \( \triangle ABC \) y \( A_C \) es el área del sector circular \( ASP \). Se tiene:
\[ \boldsymbol{(1)} \hspace{2em} A_S = A_T – 2 A_C \]Pero, \( A_T = \frac{12 \times 12}{2} = 72 \), ya que los catetos son base y altura del triángulo.
Por ser el triángulo isósceles, los ángulos \( \angle A \) y \( \angle B \) son congruentes, y por ser rectángulo, estos miden \( 45^{\circ} \) cada uno.
Luego,
\[ A_C = \frac{45}{360} ( \pi \cdot 6^2) = 4.5 \pi \]Reemplazando en (1):
\[ \begin{aligned} A_S &= A_T – 2 A_C \\[1em] &= 72 – 2(4.5 \pi) \\[1em] &= 72 – 9\pi \\[1em] &= \boldsymbol{ 3(24 – 3\pi) } \end{aligned} \]
