Problemas Resueltos - Razonamiento matemático
Problema 76
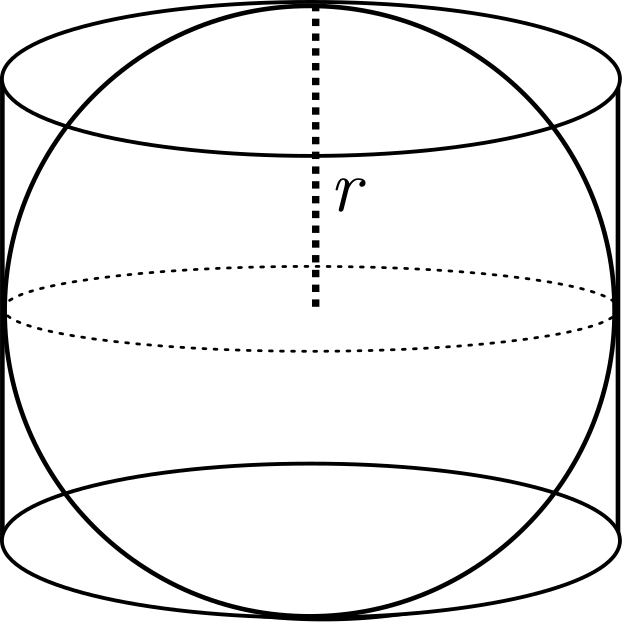
Una esfera está inscrita en un cilindro circular recto de radio \( r \) y altura \( 2r \). Entonces la razón entre el volumen de la esfera y el volumen del cilindro es:
-
\( \frac{3}{4} \)
-
\( \frac{4}{3} \)
-
\( \frac{2}{3} \)
-
\( \frac{3}{2} \)
-
\( \frac{4\pi}{3} \)
Intenta resolverlo antes de ver la respuesta...
-
\(\frac{2}{3}\)
En efecto, sean:
- \( V_e \): el volumen de la esfera
- \(V_c\): el volumen del cilindro
De acuerdo a la lección Figuras en el Espacio, tenemos que:
y
\[ \begin{aligned} V_c &= \pi r^2 h \\ &= \pi r^2 (2r) \\ &= 2 \pi r^3 \end{aligned} \]y
Luego,
\[ \begin{aligned} \frac{V_e}{V_c} &= \frac{ \frac{4}{3} \pi r^3 }{ 2 \pi r^3 } \\[2em] &= \frac{4}{ 3 \times 2 } = \boldsymbol{ \frac{2}{3} } \end{aligned} \]