Problemas Resueltos - Razonamiento matemático
Problema 35
Los números \(x\), \(y\) y \(z\) se ubican en la recta real como indica la figura:
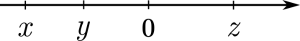
Se puede afirmar que:
-
\( xy < xz \)
-
\( xy > z \)
-
\( y^2 < x^2 \)
-
\( x^2 < z^2 \)
-
\( xy < z \)
Intenta resolverlo antes de ver la respuesta...
-
\( y^2 < x^2 \)
De acuerdo a la figura tenemos que:
Por la lección «Desigualdades», se tiene que:
\( x < y, \quad x < 0 \Rightarrow x^2 > xy \hspace{4em} \boldsymbol{(1)} \)
\( x < y, \quad y < 0 \Rightarrow xy > y^2 \hspace{4em} \boldsymbol{(2)} \)
De (1) y (2), por transitividad, se tiene que \( x^2 > y^2 \), ó, lo que es lo mismo:
De (1) y (2), por transitividad, se tiene que \( x^2 > y^2 \), ó, lo que es lo mismo: \(\boldsymbol{ y^2 < x^2 } \)
