Problemas Resueltos - Razonamiento matemático
Problema 21
En la figura, \(D\) es el punto medio de \( \overline{AC} \), \(E\) es el punto medio de \(\overline{BC}\) y \(F\) es el punto medio de \( \overline{EC} \). Entonces la pareja de triángulos semejantes es:
-
\(\triangle DEF \) y \(\triangle ABE \)
-
\(\triangle DFC \) y \(\triangle AED \)
-
\(\triangle DFC \) y \(\triangle DEF \)
-
\(\triangle AED \) y \(\triangle ABE \)
-
\(\triangle DEF \) y \(\triangle AED \)
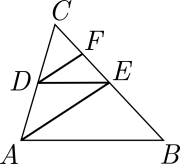
Intenta resolverlo antes de ver la respuesta...
-
\( \triangle DEF \) y \( \triangle ABE \)
Solución
\( D \) es el punto medio de \( \overline{AC} \), entonces:
\( E \) es el punto medio de \( \overline{BC} \), entonces:
Luego:
Esto nos dice que el par de segmentos \( \overline{AD} \) y \( \overline{DC} \) son proporcionales al par \( \overline{BE} \) y \( \overline{EC} \).
El teorema recíproco al teorema de Thales, nos dice que cuando esto sucede, los segmentos \(\overline{DE}\) y \( \overline{AB} \) son paralelos. En consecuencia, los ángulos \( \alpha\) y \( \alpha’ \), por ser correspondientes, son congruentes (leccion «ángulos»).

En forma análoga, por ser \( D \) el punto medio de \( \overline{AC} \), y \(F\) el punto medio de \( \overline{CE} \), los segmentos \( \overline{DF} \) y \( \overline{AE} \) son paralelos. En consecuencia, los ángulos \( \beta \) y \(\beta’ \) , por ser correspondientes, son congruentes.
Por último, por el criterio AA (lección «Propiedades de Triángulos»), los triángulos \( \triangle DEF \) y \( \triangle ABE \) son semejantes.

