Problemas Resueltos - Razonamiento matemático
Problema 186
Los números \( a \), \( b \), \( x \), \( y \), \( z \), están colocados sobre la recta real, como indica la figura.
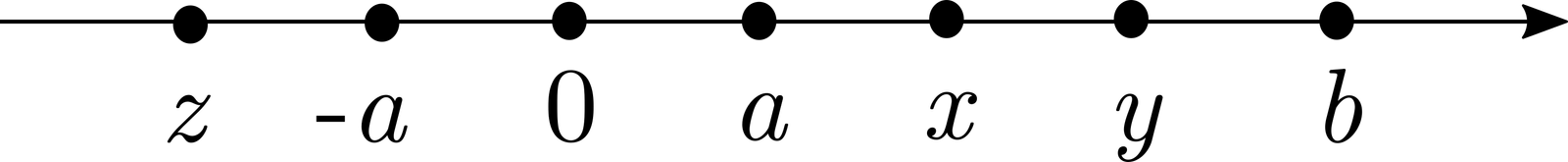
¿Cuál de las siguientes afirmaciones es falsa?
-
\( x + a > 0 \)
-
\( z + a > 0 \)
-
\( b - a > y - x \)
-
\( \frac{a - b}{z} > 0 \)
-
\( \frac{y - b}{a - x} > 0 \)
Intenta resolverlo antes de ver la respuesta...
-
\( z + a > 0 \)
En efecto:
-
\( x + a > 0 \) es verdadera, ya que:
\[ x > 0 \quad \text{ y } \quad a > 0 \Rightarrow x + a > 0 \] -
\( z + a > 0 \) es falsa, ya que para \( z = -4 \) y \( a = 1 \), tenemos la contradicción:
\[ \begin{aligned} z + a > 0 &\Rightarrow -4 + 1 > 0 \\ &\Rightarrow -3 > 0 \end{aligned} \] -
\( b – a > y – x \) es verdadera. Según el gráfico, ya la distancia del punto \( a \) al punto \( b \), que es \( b – a \), es mayor que la distancia del punto \( x \) al punto \( y \), que es \( y – x \).
-
\( \frac{a – b}{z} > 0 \) es verdadera, ya que \( a-b < 0 \) y \( z < 0 \), y el cociente de dos números negativos es un número positivo.
-
\( \frac{y – b}{a – x} > 0 \) es verdadera por el mismo argumento de d.

