Problemas Resueltos - Razonamiento matemático
Problema 145
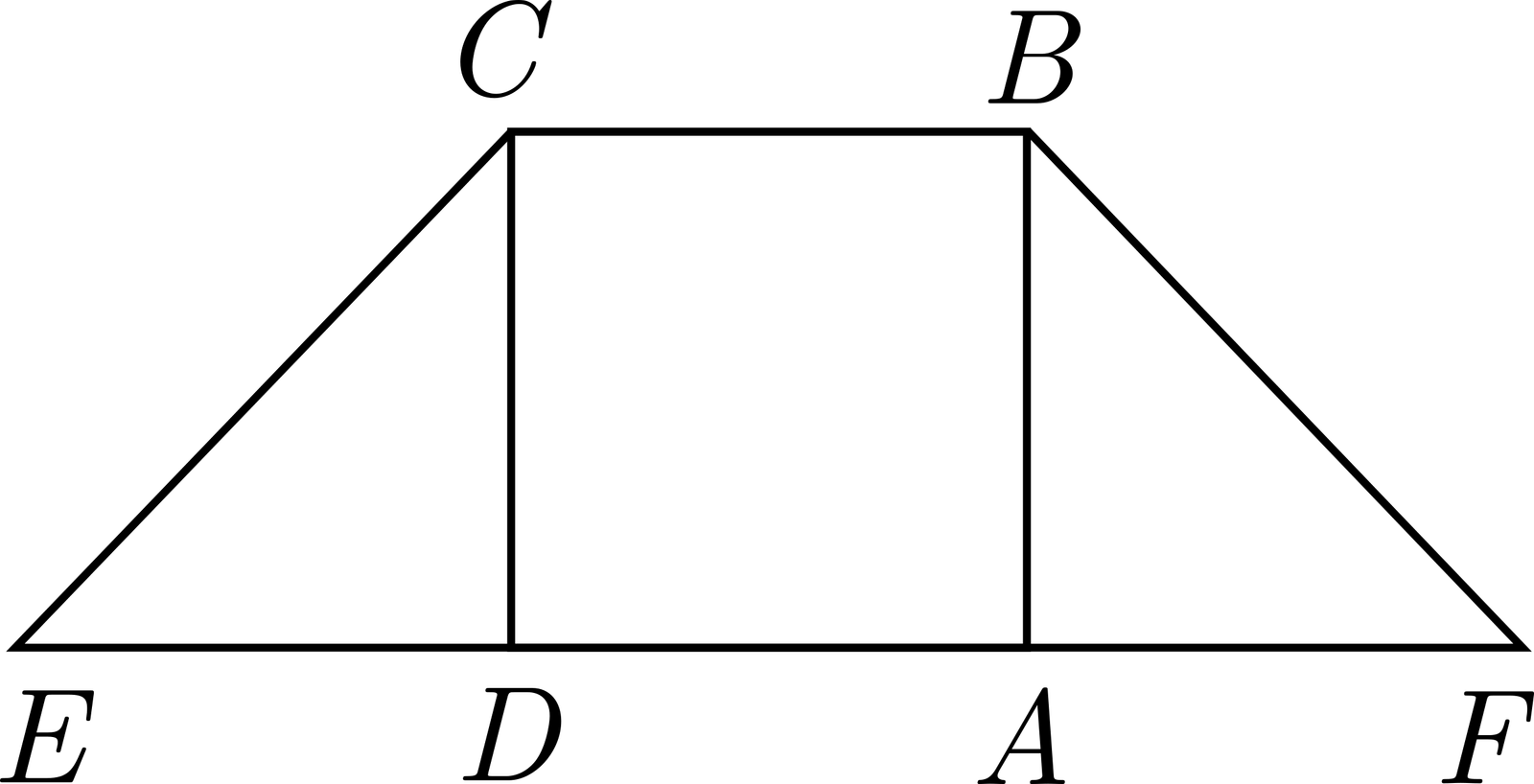
En la figura, \( ABCD \) es un cuadrado de lado 1, y los triángulos \( \triangle BAF \) y \( \triangle EDC \) son isorectángulos.
¿Cual es el perímetro total de la figura?
-
\( 6 + 2 \sqrt{2} \)
-
\( 6 \)
-
\( 8 \)
-
\( 5 \sqrt{2} \)
-
\( 4 + 2 \sqrt{2} \)
Intenta resolverlo antes de ver la respuesta...
-
\( 4 + 2 \sqrt{2} \)
\( \overline{EC} \) es la hipotenusa del triángulo \( \triangle EDC \), el cual tiene sus dos catetos de longitud 1. Luego, usando el teorema de Pitágoras:
\[ \overline{EC} = \sqrt{ 1^2 + 1^2 } = \sqrt{2} \]Similarmente, \( \overline{FB} = \sqrt{2} \), por ser la hipotenusa del triángulo rectángulo \( \triangle BAF \), el cual tiene sus dos catetos de longitud 1.
Ahora, el perímetro que pide el enunciado es el siguiente:
