Problemas Resueltos - Razonamiento matemático
Problema 132
\( \triangle ABC \) es un triángulo equilatero y su lado mide 1. \( \overline{CD} \) es su altura, \( \overline{DE} \) es perpendicular a \( \overline{AC} \). ¿Cual es la medida de \( \overline{ED} \) ?
-
\( \frac{ \sqrt{3} }{2} \)
-
\( \frac{ \sqrt{3} }{4} \)
-
\( \frac{ \sqrt{2} }{2} \)
-
\( \frac{ \sqrt{2} }{4} \)
-
\( \frac{ \sqrt{3} }{3} \)

Intenta resolverlo antes de ver la respuesta...
-
\( \frac{ \sqrt{3} }{4} \)
Los ángulos \( \angle \alpha \) y \( \angle \beta \) son congruentes por tener sus lados perpendiculares ( lección propiedades del triángulo )
Luego los triángulos rectángulos \( \triangle AED \) y \( \triangle ADC \) son semejantes ( lección propiedades del triángulo ).
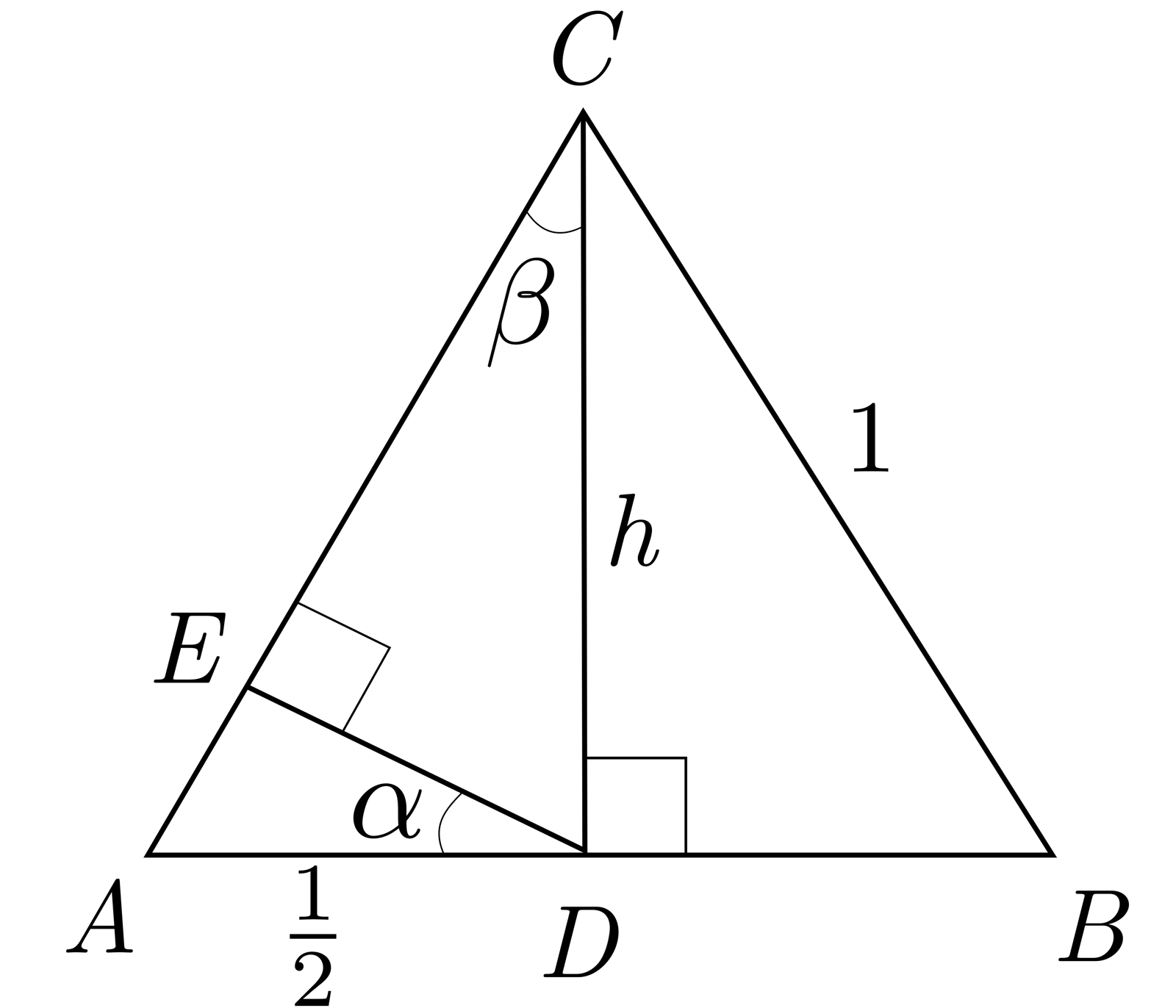
Por lo tanto:
\[ (1) \hspace{3em} \frac{\overline{ED}}{ \overline{AD} } = \frac{h}{ \overline{AC} } \]Hallemos los valores de \(\overline{AD}\) y de \( h \).
Sabemos que \( \overline{AB} = 1 \), y por ser \( \triangle ABC \) un equilátero:
\[ \overline{AD} = \frac{ \overline{AB} }{2} = \frac{1}{2} \]Aplicando el teorema de Pitágoras en el triángulo rectángulo \( \triangle ADC \):
Por último, reemplazando \( \overline{AC} = 1 \), \( \overline{AD} = \frac{1}{2} \) y \( h = \frac{ \sqrt{3} }{2} \) en (1):
