Problemas Resueltos - Razonamiento matemático
Problema 124
\( \triangle ABC \) es un triángulo rectángulo en el vértice \( C \), y \( CD \) es su altura. Si \( \overline{AD} = 4 \) y \( \overline{DB} = 3 \), ¿Cual es la medida de \( \overline{BC} \) ?
-
\( \sqrt{12} \)
-
\( \sqrt{21} \)
-
\( 12 \)
-
\( 2 \)
-
\( \sqrt{6} \)
Intenta resolverlo antes de ver la respuesta...
-
\( \sqrt{21} \)
Sean \( a = \overline{BC} \), \( b = \overline{AC} \) y \( h = \overline{CD} \).
Nos piden hallar \( a \).
Aplicando el teorema de Pitagoras en el triángulo rectángulo \( \triangle CDB \):
\[ \boldsymbol{(1)} \hspace{3em} a^2 = h^2 + 3^2 \]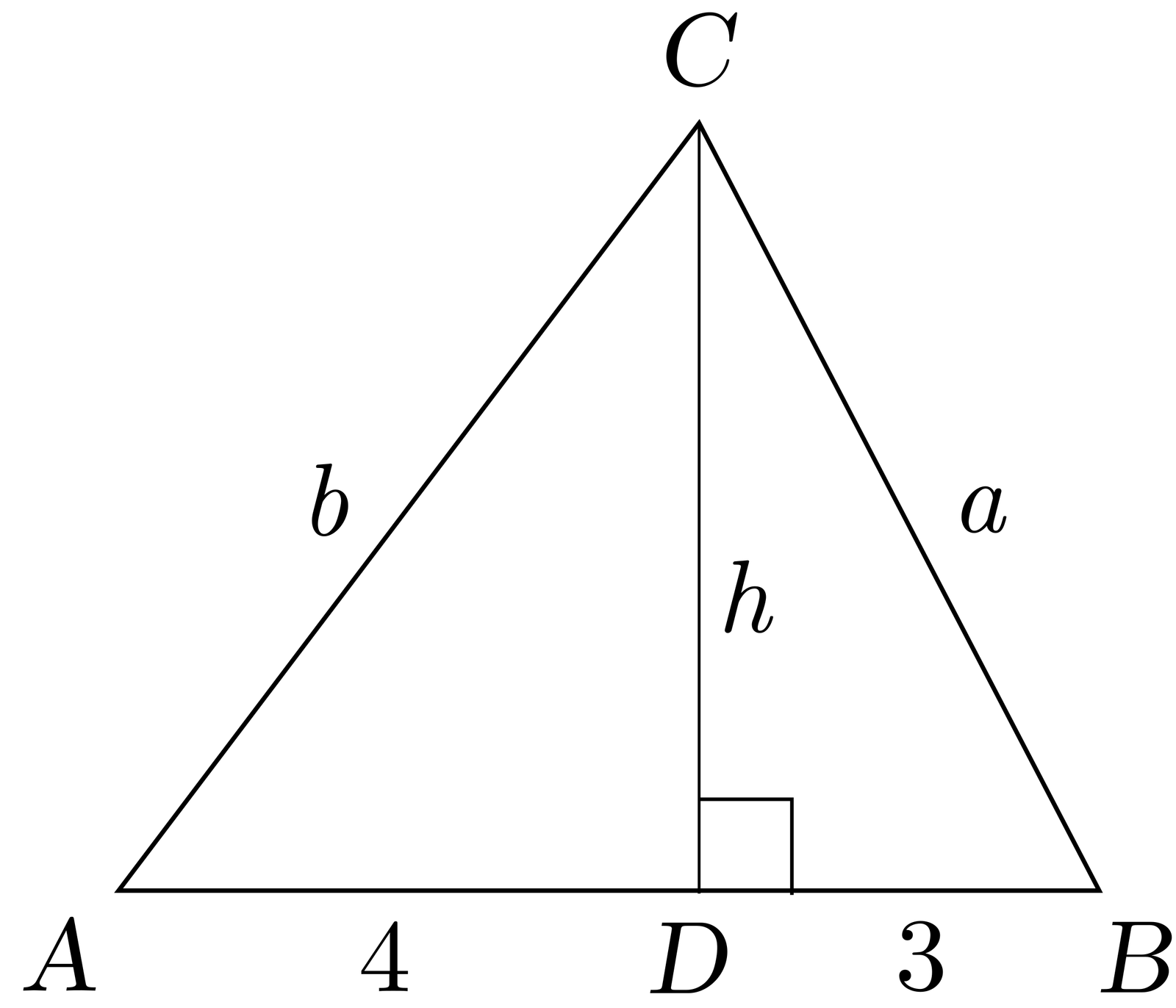
Aplicando el teorema de Pitagoras en el triángulo rectángulo \( \triangle ADC \):
\[ \boldsymbol{(2)} \hspace{3em} b^2 = h^2 + 4^2 \]Aplicando el teorema de Pitagoras en el triángulo rectángulo \( \triangle ACB \):
\[ \boldsymbol{(3)} \hspace{3em} a^2 + b^2 = (4 + 3)^2 \]Reemplazando (1) y (2) en (3):
Reemplazando \( h^2 = 12 \) en (1):
\[ \begin{aligned} a^2 = 12 + 3^2 &\Rightarrow a^2 = 12 + 9 \\[1em] &\Rightarrow a^2 = 21 \\[1em] &\Rightarrow \boldsymbol{ a = \sqrt{21} } \end{aligned} \]