Precálculo Sec.4.1 - Hipotenusa

Funciones reales y sus gráficas

Dada la función \(f(x)=\frac{x}{x+1}\), encontrar:
1. \[ f(3) \]
2. \[ f \left( 1+\sqrt{x} \right) \]
3. \[ f(2+h) - f(2) \]
4. \[ f(a+h) - f(a) \]
Dada la función \( g(x) = x + \frac{(x-2)^2}{4} \), encontrar:
1. \[ g(2) \]
2. \[ g(a+2) \]
3. \[ g(a+h)-g(a) \]

En los problemas del 3 al 8 hallar el dominio y el rango de la función dada.

\[ f(x) = \sqrt{x-9} \]
\[ g(x) = \frac{ \sqrt{16-x^2} }{3} \]
\[ h(x) = \frac{ \sqrt{x^2-4} }{2} \]
\[ u(x) = \sqrt[3]{x-2} \]
\[ f(x) = \frac{x^2-4}{x} \]
\[ y = \sqrt{ x(x-2) } \]

En los problemas del 9 al 14 hallar el dominio de la función dada.

\[ g(x) = \frac{6}{ \sqrt{9-x} -2 } \]
\[ y = \frac{1}{ \sqrt{x^2-4}-2 } \]
\[ y = \sqrt{ 4 - \frac{1}{x} } \]
\[ y = \frac{1}{4-\sqrt{1-x}} \]
\[ y = \sqrt{ \frac{x+1}{2-x} } \]
\[ y = \sqrt[4]{ \frac{x+5}{x-3} } \]

En los problemas 15 y 16, hallar el dominio, el rango y graficar la función:

\[ g(x) = \begin{cases} \left| x \right|, \; \text{ si } \; \left| x \right| \leq 1 \\[.5em] \hspace{0.9em} 1, \; \text{ si } \; \left| x \right| > 1 \end{cases} \]
\[ f(x) = \begin{cases} \hspace{1em} \sqrt{-x}, \; \text{ si } \; x < 0 \\[.5em] \hspace{2.5em} x, \; \text{ si } \; 0 \leq x \leq 2 \\[.5em] \sqrt{x-2}, \; \text{ si } \; x > 2 \end{cases} \]
Probar que:
1. Si el gráfico de \(f\) es simétrico respecto al eje Y, entonces \(f\) es par.
2. Si el gráfico de \(f\) es simétrico respecto al origen, entonces \(f\) es impar.
Si \(f(x+1) = (x-3)^2\), hallar \(f(x-1)\).
Hallar la función cuadrática:

\[ f(x)= ax^2 + bx \quad \text{tal que} \quad f(x)-f(x-1)=x,\; \forall x \in \mathbb{R} \]

\[ \begin{aligned} &f(x)= ax^2 + bx \quad \text{tal que:} \\[1em] &f(x)-f(x-1)=x,\; \forall x \in \mathbb{R} \end{aligned} \]
Un hotel tiene 40 habitaciones. El gerente sabe que cuando el precio por habitación es de 30 dólares todas las habitaciones son alquiladas, pero por cada 5 dólares de aumento una habitación se desocupa. Si el precio de mantenimiento de una habitación ocupada es de 4 dólares, expresar la ganancia del hotel como función del número \(x\) de habitaciones alquiladas.
Cuando la producción diaria no sobrepasa de 1,000 unidades de cierto artículo, se tiene una utilidad de 4,000 dólares por artículo; pero si el número de artículos producidos excede los 1,000, la utilidad, para los excedentes, disminuye en 10 dólares por cada artículo que excede los 1,000. Expresar la utilidad diaria del productor como función del número \(x\) de artículos producidos.
Una granja está sembrada de mangos a razón de 80 plantas por hectárea. Cada planta produce un promedio de 960 mangos. Por cada planta adicional que se siembre, el promedio de producción por planta se reduce en 10 mangos. Expresar la producción \(p(x)\) de mangos por hectárea como función del número \(x\) de plantas de mango sembradas por hectárea.
Para enviar cierto tipo de cajas por correo la administración exige que éstas sean de base cuadrada y que la suma de sus dimensiones (largo + ancho + altura) no supere los 150 \(cm\). Exprese el volumen de la caja, con máxima suma de sus lados, como función de la longitud del lado \(x\) de la base.
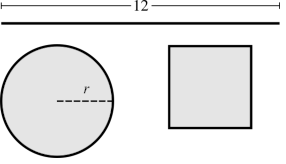
Un alambre de 12 \(m\). de largo se corta en dos pedazos.

Con uno de ellos se forma una circunferencia y con el otro un cuadrado.

Expresar el área encerrada por estas dos figuras como función del radio \(r\).

Expresar el área encerrada por estas dos figuras como función del radio \(r\).
Un triángulo isósceles tiene 36 \(cm\). de perímetro. Expresar el área del triángulo como función de la longitud \(x\) de uno de los lados iguales.
Una ventana tiene forma de un rectángulo coronado por un semicírculo.

La ventana tiene de 7 \(m\). de perímetro.

Expresar el área de la ventana como función del ancho \(x\).

Expresar el área de la ventana como función del ancho \(x\).
Un fabricante de envases construye cajas sin tapa utilizando láminas de cartón rectangulares de 80 \(cm\). de largo por 50 \(cm\). de ancho.

Para formar la caja, se hace un recorte cuadrado en cada esquina de cada lámina, luego se doblan las aletas, tal como lo indica la figura.

Expresar el volumen del envase como función de la longitud \(x\) del lado del cuadrado cortado.

Expresar el volumen del envase como función de la longitud \(x\) del lado del cuadrado cortado.
Se quiere imprimir un libro, en el cual cada página tenga 3 \(cm\). de margen superior, 3 \(cm\). de margen inferior y 2 \(cm\). de margen a cada lado.

El texto escrito debe ocupar un área de 252 \(cm^2\).

Expresar el área de cada página como función del ancho \(x\) del rectángulo impreso.

Expresar el área de cada página como función del ancho \(x\) del rectángulo impreso.

Ver Respuestas

1. \[ \frac{3}{4} \]
2. \[ \frac{1 + \sqrt{2}}{2 + \sqrt{2}} \]
3. \[ \frac{h}{3(h + 3)} \]
4. \[ \frac{h}{(a + 1) (a + h + 1)} \]
1. \[ 2 \]
2. \[ \frac{1}{4} a^2 + a + 2 \]
3. \[ \frac{h^2 + 2ah}{4} \]
Dom\((f) = [ 9, \, +\infty)\), Rang\((f) = [0, \, +\infty)\)
Dom\((g) = [-4, \, 4]\), Rang\((g) = \left[ 0, \, \frac{4}{3} \right]\)
Dom\((h) = (-\infty, \, 2] \cup [2, \, +\infty)\), Rang\((h) = [0, \, +\infty)\)
Dom\((u) =\) Rang\((u) = \mathbb{R}\)
Dom\((f) = \mathbb{R} – \{ 0 \}\), Rang\((f) = \mathbb{R}\)
Dom\((y) = (-\infty, \, 0] \cup [2, \, +\infty)\), Rang\((y) = [0, \, +\infty)\)
Dom\((g)= (-\infty, \, 9] – \{ 5 \}\)
Dom\((y) = (-\infty, \, -2] \cup [2, \, +\infty) – \{ -2 \sqrt{2}, \, 2 \sqrt{2}\}\)

\[ \begin{aligned} &\text{Dom}(y) = (-\infty, \, -2] \\[.5em] &\hspace{2em} \cup [2, \, +\infty) – \{ -2 \sqrt{2}, \, 2 \sqrt{2}\} \end{aligned} \]
Dom\((y) = (- \infty, \, 0 ) \cup \left[ \frac{1}{4}, \, +\infty \right)\)
Dom\((y) = (-\infty, \, 1] – \{ -15 \}\)
Dom\((y) = [-1, \, 2)\)
Dom\((y) = (-\infty, \, 5] \cup (3, \, + \infty)\)
Dom\((y) = \mathbb{R}\), Rang\((y) = [0, \, 1]\)
\(\text{Dom}(y) = \mathbb{R}, \, \text{Rang}(y) = [0, \, +\infty)\)

\[ f(x – 1) = (x – 5)^2 \]
\[ f(x) = \frac{1}{2} x^2 + \frac{1}{2}x \]
\[ U(x) = 226x – 5x^2 \]
\[ G(x) = \begin{cases} 4,000 x, \hspace{3em} \text{si } \; 0 \leq x \leq 1,000 \\ 4,000,000 + (x – 1,000)(14,000 – 10x), \; \text{ si } x > 1,000 \end{cases} \]

\[ \begin{aligned} G(x) = \begin{cases} 4,000 x, \\ \hspace{2em} \text{si } \; 0 \leq x \leq 1,000 \\[1em] 4,000,000 \\ \hspace{1em}+ \; (x – 1,000) \\ \hspace{2em} \times(14,000 – 10x), \\ \hspace{4em} \text{si } x > 1,000 \end{cases} \end{aligned} \]
\[ P(x) = 1,760 x – 10x^2 \]
\[ V(x) = x^2 (150 – 2x) \]
\[ A(r) = \pi r^2 + \frac{1}{4}(6 – \pi r)^2 \]
\[ A(x) = 6 (18 – x) \sqrt{x – 9} \]
\[ A(x) = \frac{x}{8}(28 – 4x – \pi x) \]
\[ V(x) = 4x (40 – x) (25 – x) \]
\[ A(x) = \frac{1}{x}(x + 4)(252 + 6x) \]