Exercises

Precalculus for Everybody

Chapter 2. The Cartesian Plane and The Line

Lines and Linear Equations
  1. Using slopes, prove that the \(A = (2, 1)\), \(B = (-4, -2)\) and \(C = (1, 1/2)\) are collinear.

In the exercises, from 2 to 9, find an equation of the line that satisfies the given conditions. Write the equation in this form: \(\boldsymbol{y = mx + b}\).

  1. Pass through (1, 3); has slope 5.
  2. Pass through the origin; has slope 5.
  3. Pass through (1, 1) and (2, 3).
  4. x-Intercept 5; y-Intercept 2
  5. Pass through (1, 3), and is parallel to the line \(5y + 3x - 6 = 0\).
  6. Pass through (4, 3), and is perpendicular to the line \(5x + y - 2 = 0\).
  7. Is parallel to \(2y + 4x - 5 = 0\), and pass through the intersection of the lines:
    \[ 5x + y = 4 \quad \text{ and } \quad 2x + 5y - 3 = 0 \]
  8. Pass through (8,-6), and intersects the axes at equal distances from the origin.
  9. Given the line \(L:\, 2y - 4x - 7 = 0\):
    1. Find the line passing through \(P = (1, 1)\), and perpendicular to \(L\).
    2. Find the distance from the point \(P = (1, 1)\) to \(L\).
  10. Using slopes, prove that the points \(A = (3, 1)\), \(B = (6, 0)\) and \(C = (4, 4)\) are the vertices of a right triangle. Find the area of the triangle.
  11. Determine which of the following lines are parallel and which are perpendicular:
    1. \[ L_1:\, 2x + 5y - 6 = 0 \]
    2. \[ L_2: \, 4x + 3y - 6 = 0 \]
    3. \[ L_3: \, -5x + 2y - 8 = 0 \]
    4. \[ L_4: \, 5x + y - 3 = 0 \]
    5. \[ L_5: \, 4x + 3y - 9 = 0 \]
    6. \[ L_6: \, -x + 5y - 20 = 0 \]
  12. Find the perpendicular bisector of the segment joining the given points:
    1. \[ (1, \, 0) \, \text{ and } \, (2, \, -3) \]
    2. \[ (-1, \, 2) \, \text{ and } \, (3, \, 10) \]
    3. \[ (-2, \, 3) \, \text{ and } \,(-2, \, -1) \]
  13. The endpoints of one of the diagonals of a rhombus are \((2, -1)\) and \((14, 3)\). Find an equation of the line that contains the other diagonal.

    Hint: the diagonals of a rhombus are perpendicular

  14. Find the distance from the origin to the line \(4x + 3y -15 = 0\).
  15. Find the distance from the point (0,-3) to the line \(5x - 12y - 10 = 0\).
  16. Find the distance from the point (1,-2) to the line \(x - 3y = 5\).
  17. Find the distance between the parallel lines\(3x - 4y = 0\) and \(3x - 4y = 10\).
  18. Find the distance between the parallel lines \(3x - y + 1 = 0\) and \(3x - y + 9 = 0\).
  19. Find the distance from the point \(Q = (6, -3)\) to the line passing through \(P = (-4, 1)\) and parallel to the line \(4x + 3y = 0\).
  20. Determine the value of \(C\) in the equation of the line \(L\): \(4x +3y + C = 0\). It is known that the distance from the point \(Q = (5, 9)\) to the line \(L\) is 4 times the distance from the point \(P = (-3, 3)\) to the line \(L\).
  21. Find the lines parallel to the line \(5x + 12y - 12 = 0\) that are 4 units away from this line.
  22. Find the equation of the tangent line to the circle \(x^2 + y^2 - 4x + 6y - 12 = 0\) at the point (-1, 1).
  23. Find the equations of the two lines passing through the point \(P = (2, -8)\), and are also tangent to the circle \(x^2 + y^2 = 34\).
  24. In the above exercise, find the points where the tangent lines make contact with the circle.
  25. Find the equation of each of the two lines parallel to the line \(2x - 2y + 5 = 0\), which are also tangent to the circle \(x^2 + y^2 = 9\).
  26. Find the equation of the tangent line to the circle \(x^2 + y^2 + 2x + 4y - 20 = 0\) at the point (2, 2).
  27. Find the equation of the circle with center \(C = (1, -1)\), and is also tangent to the line \(5x - 12y + 22 = 0\).
  28. Find the equation of the circle passing through the point $Q = (4, 0)$, and is also tangent to the line \(3x - 4y + 20 = 0\) at the point \(P = (-12/5, \,16/5)\).
  29. Find the equation of the circle passing through the points (3, 1) and (-1, 3), with center in the line \(3x - y - 2 = 0\).
  30. Both parallel lines, \(2x + y -5 = 0\) and \(2x + y +15 = 0\), are tangent to a circle. One point of tangency is \(B = (2, 1)\). Find an equation of the circle.
  31. Find an equation of the line passing through the point \(P = (8, 6)\), which also forms a triangle of area 12 with the coordinate axes.
  32. Determine the values of \(k\) and \(n\) in the equations of the lines:
    \[ L_1:kx - 2y - 3 = 0 \quad \text{and} \quad L_2:6x - 4y - n = 0, \]
    \[ \begin{aligned} &L_1: kx - 2y - 3 = 0 \text{ and} \\[1em] &L_2: 6x - 4y - n = 0, \end{aligned} \]
    1. if \(L_1\) intersects \(L_2\) in a single point.
    2. if \(L_1\) and \(L_2\) are perpendicular.
    3. if \(L_1\) and \(L_2\) are parallel and not coincident.
    4. if \(L_1\) and \(L_2\) are coincident.
  33. Determine for what values of \(k\) and \(n\) the lines:
    \[ kx + 8y + n = 0 \quad \text{ and } \quad 2x + ky - 1 = 0, \]
    \[ \begin{aligned} &kx + 8y + n = 0 \text{ and} \\[1em] &2x + ky - 1 = 0, \end{aligned} \]
    1. are parallel and not coincident.
    2. are coincident.
    3. are perpendicular.
  34. The center of a square is \(C = (1, -1)\), and one of its sides is on the line \(x-2y = -12\). Find the equations of the lines that containing the other sides.
  35. Prove that the points \(A = (1, 4)\), \(B = (5, 1)\), \(C = (8, 5)\) and \(D = (4, 8)\) are the vertices of a rhombus (a quadrilateral whose sides have equal length). Verify that the diagonals are perpendicular.
  36. Let \(a\) and \(b\) be the x-intersection and the y-intersection of a line.

    If \(a \neq 0\) and \(b \neq 0\), prove that an equation for this line is \(\frac{x}{a} + \frac{y}{b} = 1\).

  37. Roberto is playing pool in a championship.

    He must hit, without spin, the eight ball with the white ball using two sides of the table(as the figure indicates).

    If the white ball is on the point \(P = (2, 6)\), and the red ball on \(Q = (3, 2)\), find the points \(A\) and \(B\) of the sides of the table where the ball must make contact to be successful.

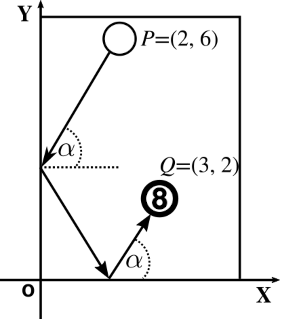
    billard table 8 ball

    If the white ball is on the point \(P = (2, 6)\), and the red ball on \(Q = (3, 2)\), find the points \(A\) and \(B\) of the sides of the table where the ball must make contact to be successful.

  1. \[ y = 5x – 2 \]
  2. \[ y = -3x \]
  3. \[ y = 2x – 1 \]
  4. \[ y = – \frac{2}{5}x + 2 \]
  5. \[ y = – \frac{3}{5} x + \frac{18}{5} \]
  6. \[ y = \frac{x}{5}+ \frac{11}{5} \]
  7. \[ y = -2x + \frac{41}{23} \]
  8. \[ x + y = 2;\,x – y = 14 \]
  9.  
    1. \[ y = – \frac{x}{2} + \frac{3}{2} \]
    2. \[ \frac{ 9 \sqrt{5}}{10} \]
  10. \[ 5 \]

  11. \(L_2\) is paralel to \(L_5\);   \(L_3\) is perpendicular to \(L_1\);   \(L_4\) is perpendicular to \(L_6\).

  12.  
    1. \[ x – 3y – 6 = 0 \]
    2. \[ x + 2y – 13 = 0 \]
    3. \[ y = 1 \]
  13. \[ y + 3x – 25 = 0 \]
  14. \[ 3 \]
  15. \[ 2 \]
  16. \[ \frac{2}{\sqrt{10}} \]
  17. \[ 2 \]
  18. \[ \frac{ 4 \sqrt{10} }{5} \]
  19. \[ \frac{28}{5} \]
  20. \[ C = -7 \; \text{ or } \; C = \frac{59}{3} \]

  21. \(5x + 12y + 40 = 0\);   \(5x + 12y – 64 = 0\)

  22. \[ 3x – 4y + 7 = 0 \]

  23. \(5x – 3y – 34 = 0\);   \(3x + 5y + 34 = 0\)

  24. \[ (5, \, -3) \; \text{ y } \; (-3, \, -5) \]
  25. \[ x – y – 3 \sqrt{2} = 0; \; x – y + 3 \sqrt{2} = 0 \]
    \[ \begin{aligned} &x – y – 3 \sqrt{2} = 0; \\[.5em] &x – y + 3 \sqrt{2} = 0 \end{aligned} \]
  26. \[ 3x + 4y – 14 = 0 \]
  27. \[ (x – 1)^2 + (y + 1)^2 = 9 \]
  28. \[ x^2 + y^2 = 16 \]
  29. \[ (x – 2)^2 + (y – 4)^2 = 10 \]
  30. \[ (x + 2)^2 + (y + 1)^2 = 20 \]
  31. \[ 3x – 2y – 12 = 0; \, 3x – 8y + 24 = 0 \]
  32.  
    1. \[ k \neq 3, \, \text{any } n \]
    2. \[ k = -\frac{4}{3}, \, \text{any } n \]
    3. \[ k = 3, \, n \neq 6 \]
    4. \[ k = 3, \, n = 6 \]
  33.  

    1. \(k = -4\)   and   \(n \neq 2\)   or   \(k = 4\)   and   \(n \neq -2\)

    2. \(k = -4\)   and   \(n = 2\)   or   \(k = 4\)   and   \(n = -2\)

    3. \(k = 0\)   and   any \(n\)

  34. \(x – 2y – 18 = 0\);   \(2x + y + 14 = 0\);   \(2x + y – 16 = 0\)

  1. \(A = \left( 0, \, \frac{14}{5} \right)\),   \(B = \left( \frac{7}{4}, \, 0\right)\)