Exercises

Precalculus for Everybody

Chapter 2. The Cartesian Plane and The Line

Equation Graphs. Symmetry and Translations

In the exercises, from 1 to 7, use the test of symmetry to determine if the graph of the equation is symmetric with respect to the X-axis, Y-axis or the origin.

  1. \[ y = x^2 \]
  2. \[ xy = 1 \]
  3. \[ \frac{x^2}{4} + \frac{y^2}{9} = 1 \]
  4. \[ \frac{x^2}{4} - \frac{y^2}{9} = 1 \]
  5. \[ y^2(2 - x) = x^3 \]
  6. \[ x^2 + y^2 + x = \sqrt{x^2+y^2} \]
  7. \[ (x^2 + y^2)^2 = x^2 - y^2 \]

In the exercises, from 8 to 16, find an equation of the circle satisfying the given conditions.

  1. Center, \((2, -1)\);   \(r = 5\).
  2. Center \((-3, 2)\);   \(r =\sqrt{5}\).
  3. Center in the origin, pass through \((-3, 4)\).
  4. Center \((1, -1)\), pasa por \((6, 4)\).
  5. Center \((1, -3)\), es tangente al eje X.
  6. Center \((-4, 1)\), es tangente al eje Y.
  7. A diameter with endpoints: \((2, 4)\)   and   \((4, -2)\).
  8. Radius \(r = 1\) pass through: \((1, 1)\)   and   \((1, -1)\).
  9. Passing through the points \((0, 0)\), \((0, 8)\)   and   \((6, 0)\).

In the exercises, from 17 to 22, prove that the equation corresponds to a circle by finding the center and the radius.

  1. \[ x^2 + y^2 - 2x - 3 = 0 \]
  2. \[ x^2 + y^2 + 4y - 4 = 0 \]
  3. \[ x^2 + y^2 + y = 0 \]
  4. \[ x^2 + y^2 - 2x + 4y - 4 = 0 \]
  5. \[ 2x^2 + 2y^2 - x + y - 1 = 0 \]
  6. \[ 16x^2 + 16y^2 - 48x - 16y - 41 = 0 \]

In the exercises 23, 24 and 25 use the translation criterion on the semi-cubical parabola(ex. 2.2.7-b) to graph the equations.

  1. \[ (y - 1)^2 = (x + 1)^3 \]
  2. \[ (x - 1)^2 = (y + 1)^3 \]
  3. \[ (y+1)^2 = (x - 1)^3 \]

In the exercises, from 26 to 28, graph the equation. Use the translation and inversion criteria, and the graph of the Agnesi witch (example 2.2.7-a).

  1. \[ (x-3)^2(y-2)=4(4-y) \]
  2. \[ (y - 3)^2(x - 2) = 4(4 - x) \]
  3. \[ (x + 3)^2(y + 2) = 4(-y) \]
  1. Y-axis
  2. Origin
  3. X-axis, Y-axis and Origin
  4. X-axis, Y-axis and Origin
  5. X-axis
  6. X-axis
  7. X-axis, Y-axis and Origin
  8. \[ (x – 2)^2 + (y + 1)^2 = 25 \]
     
  9. \[ (x + 3)^2 + (y – 2)^2 = 5 \]
     
  10. \[ x^2 + y^2 = 25 \]
     
  11. \[ (x – 1)^2 + (y + 1)^2 = 50 \]
     
  12. \[ (x – 1)^2 + (y + 3)^2 = 9 \]
     
  13. \[ (x + 4)^2 + (y – 1)^2 = 16 \]
     
  14. \[ (x – 3)^2 + (y – 1)^2 = 10 \]
     
  15. \[ (x – 1)^2 + y^2 = 1 \]
     
  16. \[ (x – 3)^2 + (y – 4)^2 = 25 \]
     
  17. Center \((1, \, 0), \; r= 2\)
  18. Center \((0, \, -2), \; r = 2 \sqrt{2}\)
  19. Center \(\left( 0, \, -\frac{1}{2} \right), \; r = \frac{1}{2} \)
  20. Center \((1, \, -2), \; r = 3\)
  21. Center \(\left( \frac{1}{4}, \, -\frac{1}{4} \right), \; r = \frac {\sqrt{10}}{4}\)
  22. Center \(\left( \frac{3}{2}, \, \frac{1}{2} \right), \; r = \frac{9}{4}\)
  23. \[ (y – 1)^2 = (x + 1)^3 \]
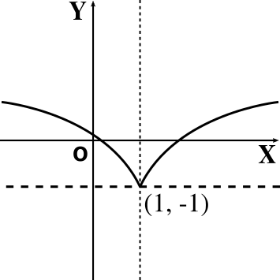
    gráfica
  24. \[ (x – 1)^2 = (y + 1)^3 \]
    gráfica
  25. \[ (y + 1)^2 = (x – 1)^3 \]
    gráfica
  26. \[ (x-3)^2 (y – 2) = 4 \left(2 -(y – 2) \right) \]
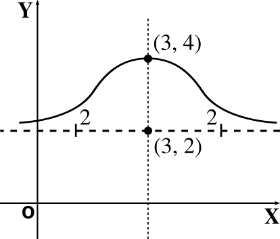
    gráfica
  27. \[ (y – 3)^2 (x – 2)= 4 \left( 2 – (x-2) \right) \]
    gráfica
  28. \[ (x + 3)^2 (y + 2) = 4 \left( 2 -(y + 2) \right) \]
    gráfica