Exercises

Precalculus for Everybody

Chapter 4. Real Functions

Trigonometric Functions

  1. Without using a calculator, find:

    1. \[ \cot \frac{5\pi}{3} \]
    2. \[ \sin \frac{7\pi}{6} \]
    3. \[ \tan \left( -\frac{\pi}{3} \right) \]
    4. \[ \sec \left( -\frac{7\pi}{6} \right) \]
    5. \[ \text{cosec} \left( -\frac{241 \pi}{6} \right) \]

  2. Find all \(\alpha \in \mathbb{R}\) such that:

    1. \[ \tan \alpha =0 \]
    2. \[ \cot \alpha =0 \]
    3. \[ \sec \alpha =0 \]
    4. \[ \text{cosec } \alpha =0 \]
    5. \[ \text{sen } \alpha = -\frac{\sqrt{3}}{2} \]

  3. Prove that:

    1. \[ \cot(\alpha + \pi) = \cot \alpha \]
    2. \[ \sec(\alpha+\pi) = -\sec \alpha \]
    3. \[ \text{cosec}(\alpha + \pi) = -\text{cosec} \alpha \]

  4. Prove that:

    1. \[ \cos(n \pi) = (-1)^n \]
    2. \[ \cos(\alpha + n\pi) = (-1)^n \cos \alpha \]
    3. \[ \sin(\alpha + n \pi) = (-1)^n \sin \alpha \]

  5. Let \(P=(x, y)\neq(0, 0)\) be a point of the plane with a distance of \(r\) from the origin. Sea \(P=(x, y)\neq(0, 0)\)   un punto del plano que está a una distancia \(r\) del origen.

    If \(L(t)\) is the point of intersection between the segment \(\overline{\text{O}P}\) and the trigonometric circle, prove that:

    1. \[ \sin t = \frac{y}{r} \]
    2. \[ \cos t = \frac{x}{r} \]
    3. \[ \tan t = \frac{y}{x},\; x \neq 0 \]
    trigonometric circle
    trigonometric circle

    If \(L(t)\) is the point of intersection between the segment \(\overline{\text{O}P}\) and the trigonometric circle, prove that:

    1. \[ \sin t = \frac{y}{r} \]
    2. \[ \cos t = \frac{x}{r} \]
    3. \[ \tan t = \frac{y}{x},\; x \neq 0 \]
  6. Find the value of \(\sin (-{23\pi/2}) \cos(31 \pi)\).

  7. If \(\alpha + \beta + \gamma=\pi\), simplify:

    1. \[ \sin( 2\alpha + \beta + \gamma ) \]
    2. \[ \sin( 2\alpha + \beta + \gamma ) + \sin(\beta + \gamma) \]

  8. We know that the period of \(y=\sin x\) is \(2\pi\), and the period of \(y=\cot x\) is \(\pi\). With that in mind, find the period of the following functions:

    1. \(f(x) = \sin(\gamma x)\),   where   \(\gamma > 0\).
    2. \(g(x) = \cot(2x)\)

  9. A circle has a radius of 18 \(cm\). Find the measure, in radians, of a central angle with an arc length of:

    1. \[ 6 \; cm \]
    2. \[ 1.8\; cm \]
    3. \[ 6 \pi \; cm \]

  10. Find the length of the arc subtended, on a 9 \(cm\). radius circle, by a central angle of:

    1. \(\frac{\pi}{6}\) radians.
    2. \(\frac{5}{4} \pi\) radians.
    3. \(50^{\circ}\).

  11. The distance of two points, \(A\) and \(B\), on the Earth's surface is given by the length of the arc formed by these points and the center of the Earth, \(C\). Since the radius of the Earth is 6.367 \(Km\), find the distance between \(A\) and \(B\) if the angle \(\angle ACB\) measures:

    1. \[ 1^{\circ}. \]
    2. \[ 30^{\circ}. \]
    3. \[ 45^{\circ}. \]
    4. \[ 80^{\circ} 45'. \]
  12. In the previous problem, if the angle \(\angle ACB\) measures \(1'\) (one minute), then the distance between \(A\) and \(B\) is a nautical mile. How many kilometers does a nautical mile have?
  13. How many radians does the minute hand of a clock turn in a time span of 20 minutes?
  14. Find the measure in degrees of the angle that is supplementary to an angle of \(\frac{\pi + 1}{2}\) radians.
  15. Two angles of a triangle measure \(\frac{\pi + 1}{2}\) and \(\frac{3\pi - 4}{8}\) radians, respectively. Find the measure in degrees of the remaining angle.

  16. In the figure, the arc \(\stackrel{\frown}{QP}\) has a length of \(\frac{7\pi}{3} \, cm\).

    Find the point \(P\).

    Arc in the cartesian plane

    Find the point \(P\).

  17. In the figure, the radius of the circle is 3 \(cm\). and the la length of the arc \(\stackrel{\frown}{QP}\) es \(2\pi\) is \(2\pi\).

    Find the point \(P\).

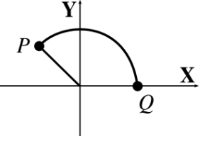
    Arc on a cartesian plane

    Find the point \(P\).

  18. The terminal side of an oriented angle in normal position is the segment \(\overline{OP}\), where O is the origin, and \(P=(-2, 6)\). If the measure of this angle is \(\alpha\) radians, find the value of: \((\sin \alpha - 3\cos \alpha)(\tan \alpha)(\sec \alpha)\).

  19. Find the value of:

    1. \[ \frac{ \sin(-750^{\circ}) }{ \cos(-150^{\circ}) } \]
    2. \[ \frac{ \cos(-1,290^{\circ}) }{ \tan(7,515^{\circ}) } \]
  20. Find the value of:
    \[ \left( \cos \frac{11 \pi}{6} + \sin \frac{26 \pi}{4} \right) \left( \tan \frac{\pi}{6} + \cos \frac{14\pi}{3} \right) \]
    \[ \begin{aligned} &\left( \cos \frac{11 \pi}{6} + \sin \frac{26 \pi}{4} \right) \\[1em] &\hspace{3em} \times \left( \tan \frac{\pi}{6} + \cos \frac{14\pi}{3} \right) \end{aligned} \]
    \[ \]
  21. Find the length of the side of a regular polygon of \(n\) sides inscribed in a circle of radius \(r\).
  22. The tires of a car have a diameter of 60 \(cm\). How many revolutions per minute does each tire spin when the car runs at 90 \(Km\). per hour?

  23. Two gears are linked by a belt, as the figure shows. The radii of the gears are 14 \(cm\). and 8 \(cm\). respectively.

    How many revolutions per second does the small gear roll when the big gear rolls 28 revolutions per second?

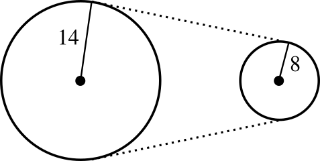
    belt with two gears of radii 14 and 8
    belt with two gears of radii 14 and 8

    How many revolutions per second does the small gear roll when the big gear rolls 28 revolutions per second?

  24. An isosceles triangle is inscribed in a circle of radius 5 \(cm\).

    Find a function that express the perimeter \(P\) of the triangle in terms of the angle \(\theta\).

    triangle inscribed in a circle

    Find a function that express the perimeter \(P\) of the triangle in terms of the angle \(\theta\).

  25. Aiming to construct a conic cup, a circular sector is cut out from a circular plate of radius 10 \(cm\).

    Find a function to express the volume of the cup in terms of the central angle \(\theta\).

    The volume of a cone is:   \(V =\frac{1}{3}\pi r^2h\)

    cone and circular plate
    cone and circular plate

    Find a function to express the volume of the cup in terms of the central angle \(\theta\).

    The volume of a cone is: \(V =\frac{1}{3}\pi r^2h\)

  26. The inclination angle of a line, which does not intersect the second quadrant, measures \(\frac{\pi}{4}\) radians. If the distance between the origin and the line is 4, find the equation of the line.

  27. Find the acute angle between the lines:

    \[ 3x + 2y=0 \quad \text{ and } \quad 5x-y + 7= 0 \]
  28. Find the equation of the line passing through the point \(Q=(2, 1)\) that generates an angle of \(\pi /4\) radians with the line \(3y + 2x + 4 = 0\) ( two solutions).
  29. The points (6, 2) and (-1, 3) are opposite vertices of a square. Find the equations of the lines that contain the sides of this square.
    1. \[ -\frac{\sqrt{3}}{3} \]
    2. \[ -\frac{1}{2} \]
    3. \[ -\sqrt{3} \]
    4. \[ -\frac{2 \sqrt{3}}{3} \]
    5. \[ -2 \]
    1. \[ \alpha = n \pi, \, n \in \mathbb{Z} \]
    2. \[ \alpha = \frac{ \pi }{2} + n \pi, \, n \in \mathbb{Z} \]

    3. none

    4. none

    5. \(\alpha = \frac{4}{3} \pi + 2n \pi\)   ó   \(\frac{5}{3} \pi + 2n \pi, \; n \in \mathbb{Z}\)

  1. \[ -1 \]
  2.  

    1. \(-\sin \alpha\)

    2. \(0\)

  3.  

    1. \(\cfrac{2\pi}{\lambda}\)

    2. \(\cfrac{\pi}{2}\)

  4.  

    1. \(\cfrac{1}{3} \, rad.\)

    2. \(\cfrac{1}{10}\, rad\)

    3. \(\cfrac{\pi}{3} \, rad\)

  5.  

    1. \(4.71 \, cm\)

    2. \(35.34 \, cm\)

    3. \(7.85 \, cm\)

  6.  

    1. \(111.13 \, km\)

    2. \(3,333.76 \, km\)

    3. \(5,000.64 \, km\)

    4. \(8,973.37 \, km\)

  7. \[ 1,852 \, km \]
  8. \[ \frac{3}{2} \pi \, rad \]

  9. \(61.35\) degrees

  10. \[ 22.5^{\circ} \]
  11. \[ \left( -\sqrt{3}, \, -1 \right) \]
  12. \[ P = \left( -\frac{3}{2}, \, \frac{3}{2} \sqrt{3} \right) \]
  13. \[ 18 \]
  14.  
    1. \[ \frac{\sqrt{3}}{3} \]
    2. \[ \frac{\sqrt{3}}{2} \]
  15. \[ \frac{\sqrt{3}}{12} \]
  16. \[ 2 r \sin \frac{\pi}{n} \]
  17. \[ \frac{2,500}{\pi} \approx 795.78 \, spins/min \]
  18. \[ 49 \, revol./sec \]
  19. \[ P(\theta)= 20 \left[ \cos \frac{\theta}{2} + \cos \frac{\theta}{2} \sin \frac{\theta}{2} \right] \]
  20. \[ V(\theta) = \frac{125}{3 {\pi}^2} {\theta}^2 \sqrt{ 4 {\pi}^2 – {\theta}^2 } \]
  21. \[ y – x + 4\sqrt{2} = 0 \]
  22. \[ \frac{\pi}{4} \]

  23. \(x – 5y + 3 = 0\);   \(5x + y – 11 = 0\)

  24. \(3x – 4y + 15 = 0\);   \(4x + 3y – 30 = 0\);   \(3x – 4y – 10 = 0\);   \(4x + 3y – 5 = 0\)