Problemas Resueltos - Razonamiento matemático
Problema 117
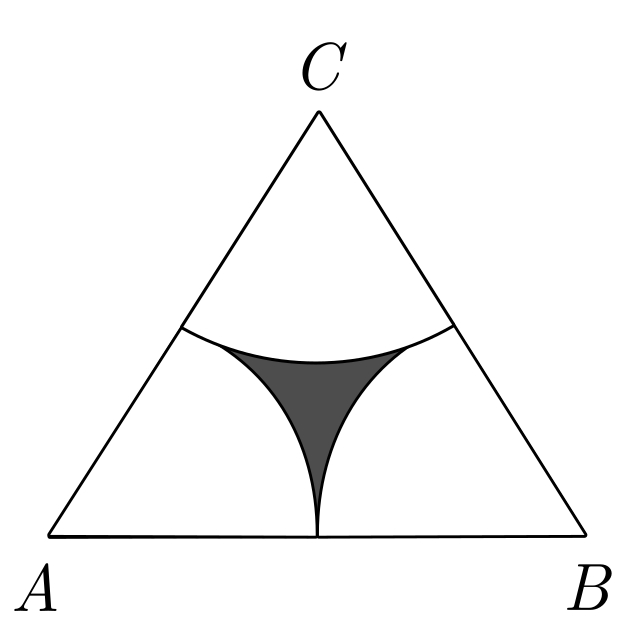
La figura adjunta es el triángulo equilátero \( \triangle ABC \) de lado 6. Se han trazado circunferencias de radio 3 y centros en sus tres vértices. ¿Cual es el área de la región sombreada?
-
\( \cfrac{ 9 \left( \pi - 2 \sqrt{3} \right) }{ 2 } \)
-
\( \cfrac{ 9 \left( 2 \sqrt{3} - \pi \right) }{ 2 } \)
-
\( \cfrac{ 3 \left( 2 \sqrt{3} - \pi \right) }{ 2 } \)
-
\( 6 \left( 2 \sqrt{3} - \pi \right) \)
-
\( 3 \left( 2\sqrt{3} - \pi \right) \)
Intenta resolverlo antes de ver la respuesta...
-
\( \cfrac{ 9 \left( 2 \sqrt{3} – \pi \right) }{ 2 } \)
Sean \(A\) el área de la región sombreada, \(A_T\) el área del triángulo \(\triangle ABC \) y \(S\) el área de uno de los tres sectores circulares de centro en un vértice.
Se tiene que:
\[ \boldsymbol{(1)} \hspace{2em} A = A_T – 3S \]Hallemos el área del triángulo \( \triangle ABC \):
La áltura \(h\) es, usando el teorema de Pitágoras:
\[ \begin{aligned} h &= \sqrt{ 6^2 – 3^2 } \\[1em] &= \sqrt{27} \\[1em] &= \sqrt{9 \times 3} \\[1em] &= 3 \sqrt{2} \end{aligned} \]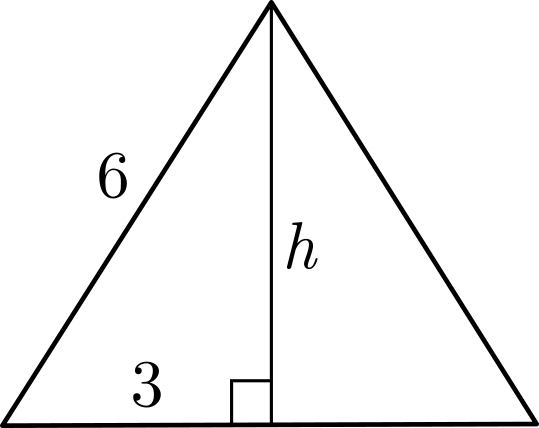
Luego,
\[ \boldsymbol{(2)} \hspace{2em} A_T = \frac{6 \times 3 \sqrt{3}}{2} = 9 \sqrt{3} \]Ahora hallemos el área del sector circular:
Cada ángulo del triángulo, por ser este equilátero, mide \( 60^{\circ} \). Por lo tanto cada uno de estos tres sectores corresponde a un ángulo de \( 60^{\circ} \), es decir, la sexta parte del círculo.
Luego,
\[ \begin{aligned} \boldsymbol{(3)} \hspace{2em} S &= \frac{ \pi (3)^2 }{6} = \frac{9\pi}{6} \\ &= \frac{3\pi}{2} \end{aligned} \]Reemplazando \((2)\) y \((3)\) en \((1)\):
\[ \begin{aligned} A &= 9\sqrt{3} – 3\left( \frac{3\pi}{2} \right) \\[1em] &= \frac{ 18 \sqrt{3} – 9\pi }{2} \\[1em] &= \boldsymbol{ \frac{ 9 \left( 2\sqrt{3} – \pi \right) }{2} } \end{aligned} \]