Trazado cuidadoso del gráfico de una función
Graficar las siguientes funciones:
-
\[ f(x) = x^3 - 6x^2 + 9x + 1 \]
-
\[ f(x) = x^4 - 2x^2 + 1 \]
-
\[ f(x) = 2x + 5x^{2/5} \]
-
\[ f(x) = \cfrac{8x}{x^2 + 1} \]
-
\[ f(x) = \cfrac{x}{ (x - 1)^{1/3} } \]
-
\[ f(x) = \cfrac{ 3 x^2 }{ x^2 + 1 } \]
-
\(f(x) = \text{ sen } x + \sqrt{3} \cos x\), en el intervalo \([-\pi, \, \pi]\) (\(f\) es periódica con periodo \(2\pi\)).
Graficar las siguientes funciones. Ellas tienen asíntotas oblicuas.
-
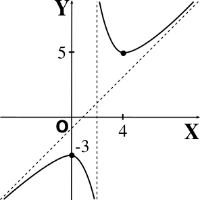
\[ f(x) = \cfrac{ x^2 - 3x + 6 }{x-2} \]
-
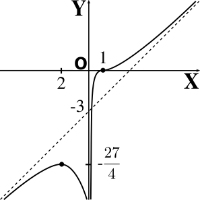
\[ f(x) = \cfrac{(x-1)^3}{x^2} \]
-
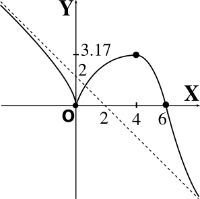
\[ f(x) = x^{2/3} (6 - x)^{1/3} \]
-
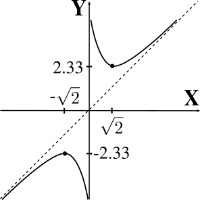
\[ x \mathrm{e}^{ \frac{1}{x^2} } \]
Ver Respuestas
Respuestas
-
-
\(\mathbb{R}\)
-
Ninguna
-
Eje Y: \((0,1)\).
Eje X: aproximadamente \((-0.104, \, 0)\)
-
Sin asíntotas
-
Máx. local: \(f(1) = 5\),
mín. local: \(f(3) = 1\)
-
Cóncava h. abajo: \((-\infty, 2]\).
Cóncava h. arriba: \([2, +\infty)\).
Pto. inflexion: \((2, 3)\)

-
-
-
\(\mathbb{R}\)
-
Ninguna
-
\((0,\, 1)\), \((-1, \, 0)\), \((1, \, 0)\)
-
Sin asíntotas
-
Máx. local: \(f(0) = 1\),
mín. local: \(f(-1) = 0\)
-
Cóncava h. arriba: \(\left( -\infty, -\frac{\sqrt{3}}{3} \right]\) y \(\left[ \frac{\sqrt{3}}{3}, +\infty \right)\),
cóncava h. abajo: \(\left[ -\frac{\sqrt{3}}{3}, \, \frac{ \sqrt{3} }{3} \right]\).
Ptos. inflexión: \(\left( -\frac{\sqrt{3}}{3}, \, \frac{4}{9} \right)\) y \(\left( \frac{\sqrt{3}}{3}, \, \frac{4}{9} \right)\)

-
Cóncava h. arriba: \(\left( -\infty, -\frac{\sqrt{3}}{3} \right]\) y \(\left[ \frac{\sqrt{3}}{3}, +\infty \right)\),
cóncava h. abajo: \(\left[ -\frac{\sqrt{3}}{3}, \, \frac{ \sqrt{3} }{3} \right]\).
Ptos. inflexión: \(\left( -\frac{\sqrt{3}}{3}, \, \frac{4}{9} \right)\) y \(\left( \frac{\sqrt{3}}{3}, \, \frac{4}{9} \right)\)
-
-
-
\(\mathbb{R}\)
-
Ninguna
-
\((0, \, 0)\), \((-4.6, \, 0)\), \((0, \, 0)\)
-
Sin asíntotas
-
Máx. local: \(f(-1) = 3\),
mín. local: \(f(0) = 0\)
-
Cóncava h. abajo: \((-\infty, \, 0]\) y \([0, \, +\infty)\)

-
Cóncava h. abajo: \((-\infty, \, 0]\) y \([0, \, +\infty)\)
-
-
-
\(\mathbb{R}\)
-
Simetría respecto al origen
-
\((0, \, 0)\)
-
Asíntotas: \(y = 0\)
-
\(f'(x) = – \cfrac{ 8 (x + 1) ( x – 1 ) }{ \left( x^2 + 1 \right)^2 }\),
Mín. local: \(f(-1) = -4\),
máx. local: \(f(1) = 4\)
-
\(f»(x) = \cfrac{ 16x \left( x^2 – 3 \right) }{ \left( x^2 + 1 \right)^3 }\),
cóncava h. abajo: \(( -\infty, \, -\sqrt{3}]\) y \([0, \, \sqrt{3})\)
cóncava h. arriba: \(\left[ -\sqrt{3}, \, 0 \right]\) y \(\left[ \sqrt{3}, \, +\infty \right)\)
Pto. de inflexión: \(\left( -\sqrt{3}, \, -2\sqrt{3} \right)\), \((0, \, 0)\), \(\left( \sqrt{3}, \, 2\sqrt{3} \right)\)

-
\(f»(x) = \cfrac{ 16x \left( x^2 – 3 \right) }{ \left( x^2 + 1 \right)^3 }\),
cóncava h. abajo: \(( -\infty, \, -\sqrt{3}]\) y \([0, \, \sqrt{3})\)
cóncava h. arriba: \(\left[ -\sqrt{3}, \, 0 \right]\) y \(\left[ \sqrt{3}, \, +\infty \right)\)
Pto. de inflexión: \(\left( -\sqrt{3}, \, -2\sqrt{3} \right)\), \((0, \, 0)\), \(\left( \sqrt{3}, \, 2\sqrt{3} \right)\)
-
-
-
Dom\((f) = \mathbb{R} – \{ 1 \}\) \(= (-\infty, \, 1) \cup (1, \, +\infty)\)
-
Ninguna simetría
-
Solo en \((0, \, 0)\)
-
Asíntota vertical: \(x = 1\)
-
\(f’ (x) = \cfrac{ 2x – 3 }{ 3 (x – 1)^{\frac{4}{3}} }\),
mín local: \(f \left( \frac{3}{2} \right)\) \()= \frac{3}{ \sqrt[3]{4} }\) \(\approx 1.9\)
-
\(f» (x) = \cfrac{ 2 (3 – x) }{ 9 (x – 1)^{\frac{7}{3}} }\),
Cóncava h. abajo: \((-\infty, \, 1)\) y \([ 3, \, +\infty )\),
cóncava h. arriba: \((1, \, 3]\).
Pto. inflexión: \(\left( 3, \, 3 \sqrt[3]{2} \right)\) \(\approx (3, \, 2.4)\)

-
\(f’ (x) = \cfrac{ 2x – 3 }{ 3 (x – 1)^{\frac{4}{3}} }\),
mín local: \(f \left( \frac{3}{2} \right)\) \()= \frac{3}{ \sqrt[3]{4} }\) \(\approx 1.9\)
-
\(f» (x) = \cfrac{ 2 (3 – x) }{ 9 (x – 1)^{\frac{7}{3}} }\),
Cóncava h. abajo: \((-\infty, \, 1)\) y \([ 3, \, +\infty )\),
cóncava h. arriba: \((1, \, 3]\).
Pto. inflexión: \(\left( 3, \, 3 \sqrt[3]{2} \right)\) \(\approx (3, \, 2.4)\)
-
-
-
Dom\((f) = \mathbb{R}\)
-
Simetría respecto al eje Y
-
Solo en \((0, \, 0)\)
-
Asíntota horizontal: \(y = 3\)
-
\(f'(x) = \cfrac{ 6x }{ \left( x^2 + 1 \right)^2 }\),
Mín. local: \(f(0) = 0\)
-
\(f»(x) = \cfrac{ 6 \left( 1 – 3x^2 \right) }{ \left( x^2 + 1 \right)^3 }\),
cóncava h. abajo: \(\left( -\infty, \, -\frac{\sqrt{3}}{3} \right)\) y \(\left( \frac{\sqrt{3}}{3}, \, +\infty \right)\),
cóncava h. arriba: \(\left( -\frac{\sqrt{3}}{3}, \, \frac{\sqrt{3}}{3} \right)\).
Pto. inflexión: \(\left( -\frac{\sqrt{3}}{3}, \, \frac{3}{4} \right)\) y \(\left( \frac{\sqrt{3}}{3}, \, \frac{3}{4} \right)\)

-
\(f»(x) = \cfrac{ 6 \left( 1 – 3x^2 \right) }{ \left( x^2 + 1 \right)^3 }\),
cóncava h. abajo: \(\left( -\infty, \, -\frac{\sqrt{3}}{3} \right)\) y \(\left( \frac{\sqrt{3}}{3}, \, +\infty \right)\),
cóncava h. arriba: \(\left( -\frac{\sqrt{3}}{3}, \, \frac{\sqrt{3}}{3} \right)\).
Pto. inflexión: \(\left( -\frac{\sqrt{3}}{3}, \, \frac{3}{4} \right)\) y \(\left( \frac{\sqrt{3}}{3}, \, \frac{3}{4} \right)\)
-
-
-
Dom\((f) = [-\pi, \, \pi ]\)
-
Ninguna simetría
-
Eje Y: \((0, \, \sqrt{3})\), eje X: \(\left( – \frac{\pi}{3}, \, 0 \right)\) y \(\left( \frac{2\pi}{3}, \, 0 \right)\)
-
Sín asíntotas
-
Mín. local: \(f \left( -\frac{5\pi}{6} \right) = -2\),
máx. local: \(f \left( \frac{\pi}{6} \right) = 2\)
-
Cóncava h. arriba: \(\left[ -\pi, \, -\frac{\pi}{3} \right]\) y \(\left[ \frac{2\pi}{3}, \, \pi \right]\),
cóncava h. abajo: \(\left[ -\frac{\pi}{3}, \, \frac{2\pi}{3} \right]\).
Pto. de inflexión: \(\left( -\frac{\pi}{3}, \, 0 \right)\) y \(\left( \frac{2\pi}{3}, \, 0 \right)\)

-
Cóncava h. arriba: \(\left[ -\pi, \, -\frac{\pi}{3} \right]\) y \(\left[ \frac{2\pi}{3}, \, \pi \right]\),
cóncava h. abajo: \(\left[ -\frac{\pi}{3}, \, \frac{2\pi}{3} \right]\).
Pto. de inflexión: \(\left( -\frac{\pi}{3}, \, 0 \right)\) y \(\left( \frac{2\pi}{3}, \, 0 \right)\)
-
-
-
Dom\((f) = \mathbb{R} – \{ 2 \}\)
-
Ninguna simetría
-
Eje Y: \((0, \, -3)\)
-
Asíntota vertical: \(x = 2\),
Asíntota oblicua: \(y = x-1\)
-
Máx. local: \(f(0) = -3\),
mín. local: \(f(4) = 5\)
-
Cóncava h. abajo: \((-\infty, \, 2)\),
cóncava h. arriba: \((2, \, +\infty)\)
Sin pto. de inflexión
-
-
-
Dom\((f) = \mathbb{R} – \{ 0 \}\)
-
Ninguna simetría
-
Eje X: \((1, \, 0)\)
-
Asín. vertical: \(x = 0\),
Asín. oblicua: \(y = x – 3\)
-
\(f'(x) = \cfrac{ (x – 1)^2 (x + 2) }{x^3}\)
Máx. local: \(f(-2) = -\frac{27}{4}\),
mín. local: no tiene
-
Cóncava hacia abajo: \((-\infty, \, 0)\) y \((0, \, 1]\)
Cóncava h. arriba: \([1,+\infty)\).
Pto. inflexión: \((1,0)\)
-
-
-
Dom\((f) = \mathbb{R}\)
-
Nínguna simetría
-
Eje Y: \((0,0)\). Eje X: \((0,0)\) y \((6,0)\)
-
Asíntota oblicua: \(y = -x + 2\)
-
\(f'(x) = \cfrac{ 4 – x }{ x^{\frac{1}{3}} (6 – x)^{ \frac{2}{3} } }\),
Mín. \(f(0) = 0\),
máx. local: \(f(4) = 2 \sqrt[3]{4}\) \(\approx 3.17\)
-
Cóncava h. arriba: \([6, \, +\infty)\)
Pto. inflexión: \((6, \, 0)\)
-
\(f'(x) = \cfrac{ 4 – x }{ x^{\frac{1}{3}} (6 – x)^{ \frac{2}{3} } }\),
Mín. \(f(0) = 0\),
máx. local: \(f(4) = 2 \sqrt[3]{4}\) \(\approx 3.17\)
-
Cóncava h. arriba: \([6, \, +\infty)\)
Pto. inflexión: \((6, \, 0)\)
-
-
-
Dom\((f) = \mathbb{R} – \{ 0 \}\)
-
Simetría respecto al origen
-
No hay intersección
-
Asín. vertical: \(x=0\),
asín. oblicua: \(y = x\)
-
\(f'(x) = \cfrac{1}{x^2} \mathrm{e}^{ \frac{1}{x^2} } \left( x + \sqrt{2} \right) \left( x – \sqrt{2} \right)\),
Máx. local: \(f \left( -\sqrt{2} \right)\) \(= -\sqrt{2} \mathrm{e}^{\frac{1}{2}}\) \(\approx -2.33\)
mín. local: \(f \left( \sqrt{2} \right)\) \(= \sqrt{2} \mathrm{e}^{\frac{1}{2}}\) \(\approx 2.33\)
-
Cóncava hacia abajo: \((-\infty, \, 0)\)
Cóncava h. arriba: \((0, \, +\infty)\).
No hay pto. inflexión
-
\(f'(x) = \cfrac{1}{x^2} \mathrm{e}^{ \frac{1}{x^2} } \left( x + \sqrt{2} \right) \left( x – \sqrt{2} \right)\),
Máx. local: \(f \left( -\sqrt{2} \right)\) \(= -\sqrt{2} \mathrm{e}^{\frac{1}{2}}\) \(\approx -2.33\)
mín. local: \(f \left( \sqrt{2} \right)\) \(= \sqrt{2} \mathrm{e}^{\frac{1}{2}}\) \(\approx 2.33\)
-
Cóncava hacia abajo: \((-\infty, \, 0)\)
Cóncava h. arriba: \((0, \, +\infty)\).
No hay pto. inflexión
-
