Precálculo Sec. 4.2

Funciones trigonométricas

1. Sin usar calculadora hallar:

   1. \[ \cot \frac{5\pi}{3} \]
   2. \[ \text{sen} \frac{7\pi}{6} \]
   3. \[ \tan \left( -\frac{\pi}{3} \right) \]
   4. \[ \sec \left( -\frac{7\pi}{6} \right) \]
   5. \[ \text{cosec} \left( -\frac{241 \pi}{6} \right) \]

2. Hallar todos los \(\alpha \in \mathbb{R}\) tales que:

   1. \[ \tan \alpha =0 \]
   2. \[ \cot \alpha =0 \]
   3. \[ \sec \alpha =0 \]
   4. \[ \text{cosec } \alpha =0 \]
   5. \[ \text{sen } \alpha = -\frac{\sqrt{3}}{2} \]

3. Probar que:

   1. \[ \cot(\alpha + \pi) = \cot \alpha \]
   2. \[ \sec(\alpha+\pi) = -\sec \alpha \]
   3. \[ \text{cosec}(\alpha + \pi) = -\text{cosec} \alpha \]

4. Probar que:

   1. \[ \cos(n \pi) = (-1)^n \]
   2. \[ \cos(\alpha + n\pi) = (-1)^n \cos \alpha \]
   3. \[ \text{sen}(\alpha + n \pi) = (-1)^n \text{sen} \alpha \]

5. Sea \(P=(x, y)\neq(0, 0)\)   un punto del plano que está a una distancia \(r\) del origen.

   Si \(L(t)\) es el punto de intersección del rayo \(\overline{\text{O}P}\) con la circunferencia unitaria, probar que:

   1. \[ \text{sen} t = \frac{y}{r} \]
   2. \[ \cos t = \frac{x}{r} \]
   3. \[ \tan t = \frac{y}{x},\; x \neq 0 \]

   

   

   Si \(L(t)\) es el punto de intersección del rayo \(\overline{\text{O}P}\) con la circunferencia unitaria, probar que:

   1. \[ \text{sen} t = \frac{y}{r} \]
   2. \[ \cos t = \frac{x}{r} \]
   3. \[ \tan t = \frac{y}{x},\; x \neq 0 \]
6. Hallar el valor de   \(\text{sen} (-{23\pi/2}) \cos(31 \pi)\).

7. Si \(\alpha + \beta + \gamma=\pi\),   simplificar:

   1. \[ \text{sen}( 2\alpha + \beta + \gamma ) \]
   2. \[ \text{sen}( 2\alpha + \beta + \gamma ) + \text{sen}(\beta + \gamma) \]

8. Conociendo que el periodo de   \(y=\text{sen} x\)   es   \(2\pi\)   y el de   \(y=\cot x\)   es   \(\pi\), hallar el periodo de las funciones:

   1. \(f(x) = \text{sen}(\gamma x)\),   donde   \(\gamma\)   es una constante mayor que \(0\).
   2. \(g(x) = \cot(2x)\)

9. Una circunferencia tiene un radio de 18 \(cm\). Hallar la medida en radianes de un ángulo determinado por un arco de longitud:

   1. \[ 6 \; cm \]
   2. \[ 1.8\; cm \]
   3. \[ 6 \pi \; cm \]

10. Hallar la longitud de un arco subtendido en una circunferencia de 9 $cm$ de radio por un ángulo central de:

    1. \(\frac{\pi}{6}\) radianes.
    2. \(\frac{5}{4} \pi\) radianes.
    3. \(50^{\circ}\).

11. La distancia entre dos puntos \(A\) y \(B\) sobre la tierra se mide a lo largo de la circunferencia que pasa por \(A\) y \(B\) y tiene por centro \(C\), el centro de la tierra. Si el radio de la tierra es, aproximadamente, 6,367 \(Km\)., hallar la distancia entre \(A\) y \(B\) si el ángulo \(\angle ACB\) mide:

    1. \[ 1^{\circ}. \]
    2. \[ 30^{\circ}. \]
    3. \[ 45^{\circ}. \]
    4. \[ 80^{\circ} 45'. \]
12. En el problema anterior, si el ángulo \(\angle ACB\) mide \(1'\) (un minuto), entonces la distancia entre \(A\) y \(B\) es de una milla náutica. ¿Cuántos $Km$. tiene una milla náutica?
13. ¿Cuántos radianes gira el minutero de un reloj en un lapso de 20 minutos?
14. Hallar la medida en grados de un ángulo que es suplemento de un ángulo de \(\frac{\pi + 1}{2}\) radianes.
15. Dos ángulos internos de un triángulo miden \(\frac{\pi + 1}{2}\)   y   \(\frac{3\pi - 4}{8}\) radianes. Hallar la medida, en grados, del tercer ángulo.

16. En la figura, el arco \(\stackrel{\frown}{QP}\) tiene una longitud de \(\frac{7\pi}{3} \, cm\).

    Hallar el punto \(P\).

    

    Hallar el punto \(P\).

17. En la figura, el radio de la circunferencia es 3 \(cm\). y la longitud del arco \(\stackrel{\frown}{QP}\) es \(2\pi\).

    Hallar el punto \(P\).

    

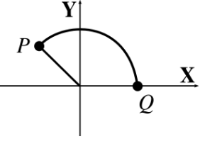
    Hallar el punto \(P\).

18. El lado terminal de un ángulo orientado en posición normal es el rayo \(\overline{OP}\), donde O es el origen y \(P=(-2, 6)\). Si la medida de este ángulo es \(\alpha\) radianes, hallar el valor de:   \((\text{sen} \alpha - 3\cos \alpha)(\tan \alpha)(\sec \alpha)\).

19. Hallar el valor de:

    1. \[ \frac{ \text{sen}(-750^{\circ}) }{ \cos(-150^{\circ}) } \]
    2. \[ \frac{ \cos(-1,290^{\circ}) }{ \tan(7,515^{\circ}) } \]
20. Hallar el valor de:
    \[ \left( \cos \frac{11 \pi}{6} + \text{sen} \frac{26 \pi}{4} \right) \left( \tan \frac{\pi}{6} + \cos \frac{14\pi}{3} \right) \]
    \[ \begin{aligned} &\left( \cos \frac{11 \pi}{6} + \text{sen} \frac{26 \pi}{4} \right) \\[1em] &\hspace{3em} \times \left( \tan \frac{\pi}{6} + \cos \frac{14\pi}{3} \right) \end{aligned} \]
    \[ \]
21. Hallar la longitud del lado de un polígono regular de \(n\) lados inscrito en una circunferencia de radio \(r\).
22. El neumático de un automóvil tiene un diámetro de 60 \(cm\). ¿A cuántas revoluciones por minuto gira la llanta cuando el automóvil viaja a 90 \(Km\). por hora?

23. Una banda enlaza a dos poleas, como indica la figura. Los radios de las poleas son de 8 \(cm\). y 14 \(cm\)., respectivamente.

    ¿A cuántas revoluciones por segundo gira la polea pequeña cuando la grande gira a razón de 28 revoluciones por segundo?

    

    

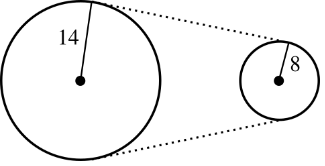
    ¿A cuántas revoluciones por segundo gira la polea pequeña cuando la grande gira a razón de 28 revoluciones por segundo?

24. Un triángulo isósceles se inscribe en un círculo de radio 5 \(cm\).

    Hallar una función que exprese el perímetro \(P\) del triángulo en términos del ángulo \(\theta\).

    

    Hallar una función que exprese el perímetro \(P\) del triángulo en términos del ángulo \(\theta\).

25. De una lámina circular de radio 10 \(\)\(cm\). se corta un sector para construir una copa cónica.

    Hallar una función que exprese el volumen de la copa en términos del ángulo central \(\theta\).

    El volumen del cono es:   \(V =\frac{1}{3}\pi r^2h\)

    

    

    Hallar una función que exprese el volumen de la copa en términos del ángulo central \(\theta\).

    El volumen del cono es: \(V =\frac{1}{3}\pi r^2h\)

26. El ángulo de inclinación de una recta que no intersecta el segundo cuadrante es de \(\frac{\pi}{4}\) rad. Hallar su ecuación sabiendo que su distancia al origen es de 4.

27. Hallar el ángulo agudo formado por las rectas:

    \[ 3x + 2y=0 \quad \text{ y } \quad 5x-y + 7= 0 \]
28. Hallar la ecuación de la recta que pasa por el punto \(Q=(2, 1)\) y forma un ángulo de \(\pi /4\) rads. con la recta   \(3y + 2x + 4 = 0\) ( dos soluciones).
29. Los puntos \((6, \, 2)\)   y   \((-1, 3)\) son dos vértices opuestos de un cuadrado. Hallar las ecuaciones de las rectas donde están los lados del cuadrado.